My friend sent me this picture while I was pooping the other day and being that I am always down for some fun math puzzles, I decided to give it a shot. At first glance it is very obvious there are extraneous bits of information thrown in that won’t necessarily help me find the answer. But let’s entertain the idea that we can glimpse some info and see if they are applicable in any way. The beer’s temperature is 489.67 °R, which is 30 °F. This is right above the freezing temperature of beer which is 28 °F. Given that ice cannot make a drink colder than 32 °F (at least not normal ice placed within the drink), we are to assume it is the cold temperature of the outside that has cooled the drink to 30 °F. The picture shows a sign of Lower Downtown Denver Historic District. So going off of some year-round temperature charts of Denver, Colorado, we can see that the outdoor temperature is roughly 30 degrees in March on average. Mercury is not in retrograde currently in 2023 and does not begin till April. The last time Mercury was in retrograde in March was in 2020. So we have isolated this scenario to the year and approximate time of year. Next, we take a look into whether the fluid properties are of any use. Given that there are no time units, we cannot effectively use flowrates to determine length of travel. So the diameter dimensions doesn’t seem to be useful (I do want to note the diameter appears to be consistent with typical beer bongs I’ve researched, which claim to be at max least an inch in diameter). So far these pieces of information do not seem helpful. So let’s continue.

All the height measurements mentioned in this problem appear to be at 45 inches. 0.000617171 nautical miles is approximately 45 inches. Given that Bertram’s is 45 inches from the ground, I want to assume he is kneeling or squatting in some way. I measured my mouth height from a kneeling position and it was approximately 43 inches but I am on the shorter side. Nowhere in the problem is it suggested that Bertram or Bill are standing up. Given that they must be legally drinking adults, Bertram would have to be a dwarf or midget in order to be both standing and have a mouth height of 45 inches (note: dwarfs get drunk much faster due to their smaller body mass. So beer bongs are not advised for them). This is where things get interesting. Beth is stated to be standing and holding the phone at mouth height. So unlike what you might think, her phone is not necessarily at the same height as Bertram’s mouth. Since Beth is definitely standing while Bertram may not be. We only know that the two are the same height when they are in the same posture. This means she is likely to be filming at an extra 18 inches height upwards from the 45 inches that Bertram’s mouth is at. This is taking into account of the average women’s leg lengths for their approximate body heights.

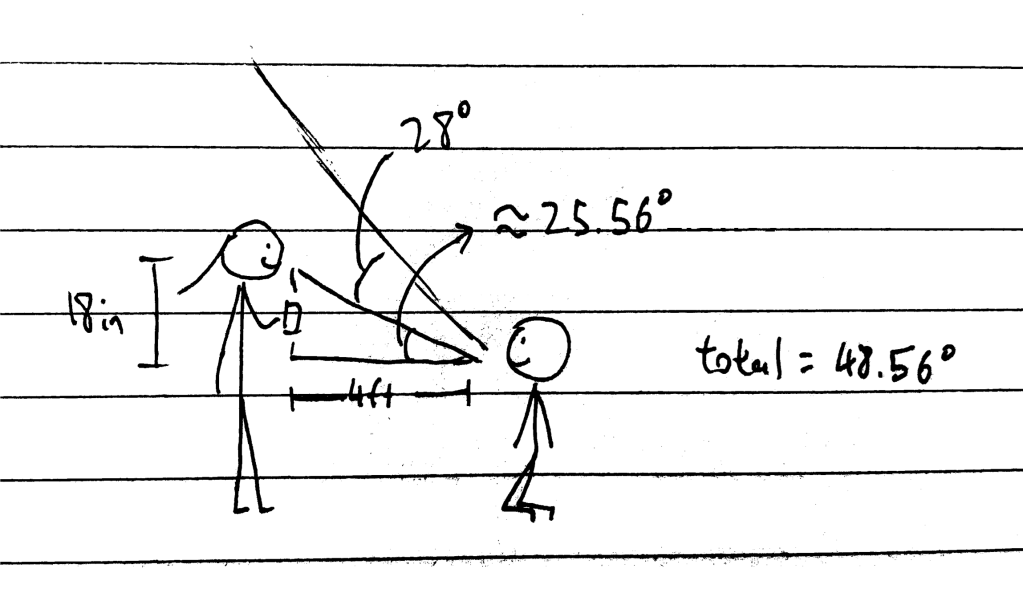
So what Beth perceives as 28 degrees means the actual angle of the mouth to funnel is probably more like 49 degrees… is what I would say if it weren’t for a crucial fact we’re missing. The problem says mouth to funnel, in which the funnel is at the top of the beer bong being held by Bill. In this scenario this angle is thus irrelevant because the tube is not straight and the funnel can be held at a large variety of angles and we still would not have a better sense on the actual length of the tube. Besides, we still have no information regarding Bertram’s location in respect to Bill.

Typically, for the fastest delivery of beer traveling along a tube downwards to a target that is NOT directly beneath it, you would want to utilize a brachistochrone curve. A brachistochrone curve is the optimal path for a curve of descent. The beer bong is likely to naturally take the form of such a curve to some extent. We are to assume Bill and Bertram are professionals of their craft and know what they’re doing. So let’s see what other information we have to go off of. We know we are in Denver. According to the Denver Zoning Codes, a building story is 14 ft. We have no real conclusion on what floor Bill is currently on but to apply Occam’s razor real quick, let’s assume the first floor. Looking at pictures of some balconies in downtown Denver, they all look significantly higher than 14 ft so this makes approximations dodgy at best. I also want to point out that for some reason the problem capitalizes balcony, leading me to believe this is a specific place or that there is a specific location named “Balcony” that I do not know about. After a quick search I couldn’t really find anything. So let’s just go with 14 ft then. For a brachistochrone curve with a height of 14 ft, the curve will reach a parallel angle with the ground after 34 ft (rounded to the nearest integer as the problem requested). I did this with very accurate math shown below.

At the end of the day, this is just a very shitty approximation of an answer to a very shitty math problem that probably isn’t meant to be taken seriously. There really aren’t that many useful pieces of information provided that can actually give an idea of what approach to take. There are many almost relevant pieces of data, but there’s always a little missing piece that robs us of a definitive answer.